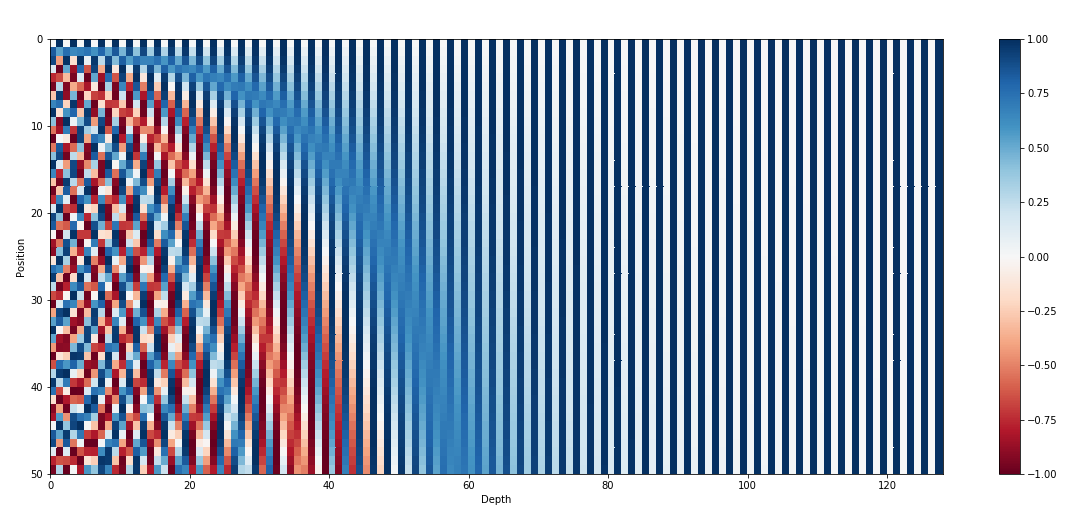
LLaMA中使用的Positional Embedding

2023年07月20日

前言

在第三次實驗室新生訓練時，講者用心介紹有關transformer training的過程，並且留了一個小作業，就是觀察LLaMA中positional encoding是使用了甚麼的技術，還有trace code的部分。而positional encoding也是在介紹transformer時，容易被忽略的一個細節。

Positional Encoding 簡介

由於transformer每次都是一整句話讀進去input，他不像RNN或VAE是透過時間序列，照順序傳入model，所以說幫transformer的input embedding做positional encoding是一件必要的事情。舉個簡單的例子，

I Am that I Am.

如果是VAE或RNN，就會一個字一個字傳進model，而transformer則是一次傳入一整句，而如果一次傳入一整句，transformer計算關係度時，就無法判別哪個或哪個比較有關係。

所以transformer需要Positional Encoding，而Positional Encoding可以分成:
1. 絕對位置編碼:
最直覺的做法就是直接對input embedding加上index，但這種做法有個壞處，當index很大時，可能會影響input embedding的內容。
2. 相對位置編碼:
由於input embedding是浮點數，透過相對位置編碼的做法可以改善絕對位置編碼花費多餘空間和normalize的問題。像是Self-Attention with Relative Position Representations這篇，他透過相對位置編碼來減少weight matrix的運算。
3. 融合式:
這個做法的觀點是，乍看是用上絕對位置編碼，但是透過transformer的計算後，最後結果與相對位置有關。這類型的方法，多半仰賴於內積時對絕對位置相減(或是說指數相除)。例如:
(a) 三角函數型: 就是Attention is All You Need那篇的方法。
(b) RoPE(Rotary Position Embedding): 出於RoFormer: Enhanced Transformer with Rotary Position Embedding的方法。這方法的特色在於使用複變函數，而LLaMA就是用RoPE的做法。
三角函數型的方法與RoPE相比，缺點在於說他只能算出相對距離關係，不能確定說字之間的方向關係。

LLaMA使用的Positional Embedding

LLaMA使用的Positional Embedding就是RoPE，我個人認為是融合了絕對位置編碼和相對位置編碼，硬要分的話就是絕對位置編碼。其方法很簡單，就下列的式子:
RoPE演算法
如果有修過通訊原理的話，應該很不陌生，兩個複數內積，其實就是將其中一個複數變成共厄複數後相乘再取實部，而複數與共厄複數相乘，在指數就是相減，RoPE透過將絕對位置編碼進歐拉數中，並透過transformer的計算，巧妙將output留下相對位置訊息。

RoPE Code分析

我們看到github: https://github.com/facebookresearch/llama/blob/main/llama/model.py#L56

#......
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    t = torch.arange(end, device=freqs.device)  # type: ignore
    freqs = torch.outer(t, freqs).float()  # type: ignore
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs)  # complex64
    return freqs_cis


def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
    ndim = x.ndim
    assert 0 <= 1 < ndim
    assert freqs_cis.shape == (x.shape[1], x.shape[-1])
    shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
    return freqs_cis.view(*shape)


def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
    return xq_out.type_as(xq), xk_out.type_as(xk)
#......

上面就是RoPE中最重要的3個function。在funciton precompute_freqs_cis中，就是提前計算絕對位置的歐拉數，也就是和。
function apply_rotary_emb就是計算前一小節RoPE理論中，分別計算和後，將其轉成和，未來在transformer時就會直接做內積。
而在function apply_rotary_emb有用到function reshape_for_broadcast，function reshape_for_broadcast的用途就是將xq_，xk_和freqs_cis弄成相同形狀，才能進一步對矩陣逐元素相乘。

心得

這次的作業中，難得看到機器學習中用到訊號處理的方法。其實在之前，我一直覺得資工和通訊本來就很有關係，也覺得這類的數學很有趣。我也很推薦別人如果有閒暇時間，去修個dsp或影像處理，都是不錯的投資。

LLaMA中使用的Positional Embedding

前言

Positional Encoding 簡介

LLaMA使用的Positional Embedding

RoPE Code分析

心得

Reference